NonlinearEquality Example

GTSAM Copyright 2010-2018, Georgia Tech Research Corporation,
Atlanta, Georgia 30332-0415
All Rights Reserved
Authors: Frank Dellaert, et al. (see THANKS for the full author list)

See LICENSE for the license information

NonlinearEquality example using a simple Pose2 chain
Author: Frank Dellaert (Python)

This notebook illustrates the use of the NonlinearEquality factor to clamp certain variables to a known value. This is the preferred way to work with known values, as the alternative of adding strong priors can make the system ill-conditioned.

Below we build a 7-pose Pose2 SLAM chain with only between factors. We compare marginal covariances for three different prior strengths, then replace the prior with a hard NonlinearEqualityPose2, and finally remove the first pose while converting the first between factor into an equivalent prior on X(2) to show the marginals match.

1. Setup and Imports¶

Install GTSAM if running in Colab, then import the needed modules.

import numpy as np
import matplotlib.pyplot as plt
import gtsam
import gtsam.utils.plot as gtsam_plot
from gtsam.symbol_shorthand import X

np.set_printoptions(precision=3, suppress=True)

2. Problem Setup¶

We use a 7-pose chain with identical odometry measurements and a simple initial guess. The only factors are a prior (or a NonlinearEquality) on the first pose and between factors connecting consecutive poses.

NUM_POSES = 7
PRIOR_POSE = gtsam.Pose2(0.0, 0.0, 0.0)
ODOM = gtsam.Pose2(2.0, 0.0, 0.1)
BETWEEN_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.2, 0.2, 0.1]))

def build_initial(drop_first=False, fixed_first=False):
    initial = gtsam.Values()
    if fixed_first:
        current = PRIOR_POSE
    else:
        current = PRIOR_POSE.compose(gtsam.Pose2(0.3, -0.2, 0.1))
    if not drop_first:
        initial.insert(X(1), current)
    for i in range(2, NUM_POSES + 1):
        current = current.compose(ODOM)
        initial.insert(X(i), current)
    return initial

def optimize_graph(graph, initial, use_qr=False):
    params = gtsam.LevenbergMarquardtParams()
    if use_qr:
        params.setLinearSolverType("MULTIFRONTAL_QR")
    optimizer = gtsam.LevenbergMarquardtOptimizer(graph, initial, params)
    return optimizer.optimize()

def plot_marginals(ax, result, marginals, pose_indices, title):
    for i in pose_indices:
        gtsam_plot.plot_pose2_on_axes(
            ax,
            result.atPose2(X(i)),
            axis_length=0.3,
            covariance=marginals.marginalCovariance(X(i)),
        )
    ax.set_title(title)
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_aspect("equal", adjustable="box")

3. Comparing Prior Strengths¶

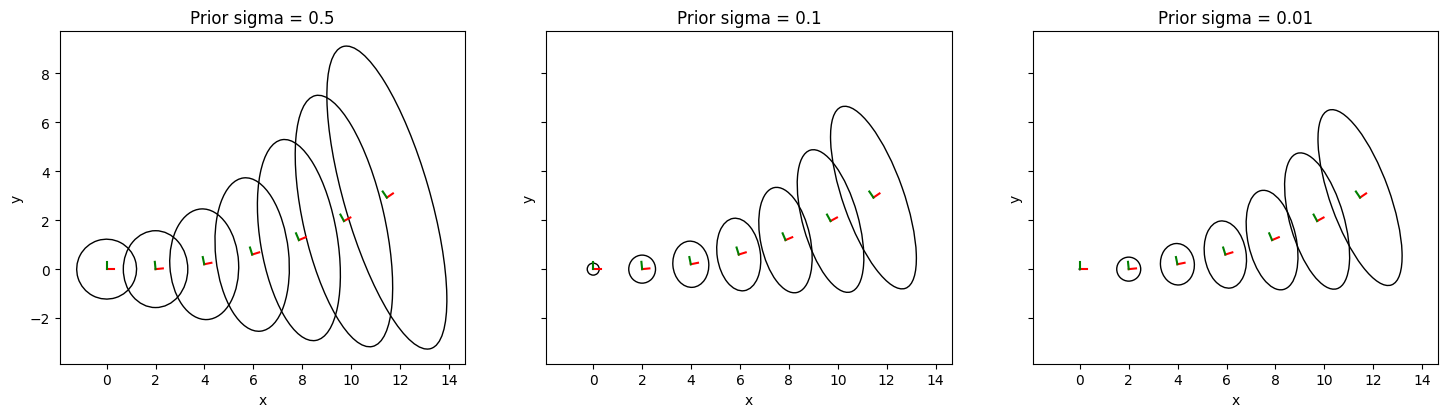
We solve the same chain three times with different prior standard deviations. Smaller sigmas mean a stronger prior.

deg20 = np.deg2rad(20)
prior_sigmas = [0.5, 0.1, 0.01]
prior_results = []

for sigma in prior_sigmas:
    prior_noise = gtsam.noiseModel.Diagonal.Sigmas(np.array([sigma, sigma, sigma*deg20]))
    graph = gtsam.NonlinearFactorGraph()
    graph.add(gtsam.PriorFactorPose2(X(1), PRIOR_POSE, prior_noise))
    for i in range(1, NUM_POSES):
        graph.add(gtsam.BetweenFactorPose2(X(i), X(i + 1), ODOM, BETWEEN_NOISE))
    initial = build_initial()
    result = optimize_graph(graph, initial)
    marginals = gtsam.Marginals(graph, result)
    prior_results.append((sigma, result, marginals))

fig, axes = plt.subplots(1, 3, figsize=(15, 4), sharex=True, sharey=True)
for ax, (sigma, result, marginals) in zip(axes, prior_results):
    plot_marginals(
        ax,
        result,
        marginals,
        pose_indices=range(1, NUM_POSES + 1),
        title=f"Prior sigma = {sigma}",
    )
plt.tight_layout()
plt.show()

4. Replacing the Prior with a NonlinearEquality¶

Here we fix the first pose exactly using NonlinearEqualityPose2, which acts as a hard constraint.

graph_eq = gtsam.NonlinearFactorGraph()
graph_eq.add(gtsam.NonlinearEqualityPose2(X(1), PRIOR_POSE))
for i in range(1, NUM_POSES):
    graph_eq.add(gtsam.BetweenFactorPose2(X(i), X(i + 1), ODOM, BETWEEN_NOISE))
initial_eq = build_initial(fixed_first=True)
result_eq = optimize_graph(graph_eq, initial_eq, use_qr=True)
marginals_eq = gtsam.Marginals(graph_eq, result_eq)

fig, ax = plt.subplots(1, 1, figsize=(6, 5))
plot_marginals(
    ax,
    result_eq,
    marginals_eq,
    pose_indices=range(1, NUM_POSES + 1),
    title="NonlinearEquality on X1",
)
ax.set_xlim(-3, 14)
ax.set_ylim(-3, 7)
plt.tight_layout()
plt.show()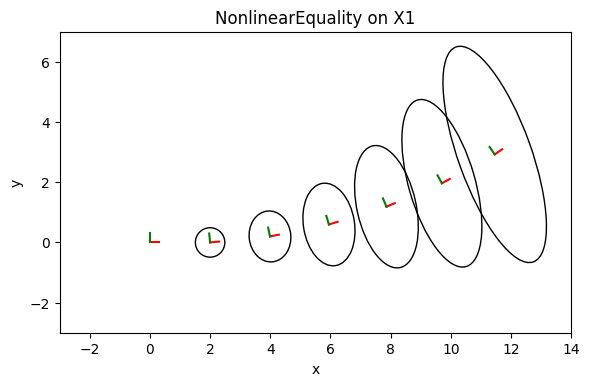

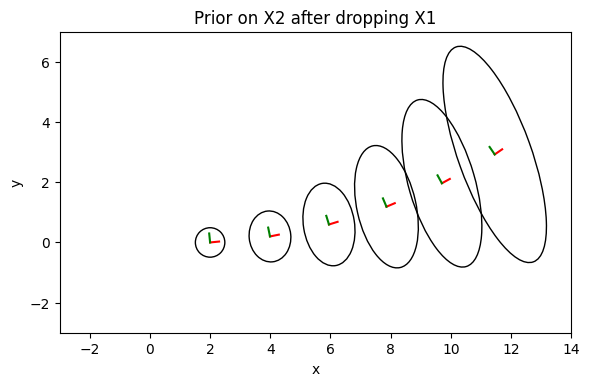
5. Showing equivalence with a smaller optimization problem.¶

To convince yourself that this is doing the right thing, let us now undertake a different way of fixing a variable. Below we show that this yields exactly the same marginals. In particular, we optimize only over 6 variables now, omitting X(1). With X(1) fixed, we can convert the “between” measurement from X(1) to X(2) into a prior on X(2) with the same noise. We drop X(1) entirely, add that equivalent prior, then compare marginals.

graph_x2 = gtsam.NonlinearFactorGraph()
prior_pose_2 = PRIOR_POSE.compose(ODOM)
graph_x2.add(gtsam.PriorFactorPose2(X(2), prior_pose_2, BETWEEN_NOISE))
for i in range(2, NUM_POSES):
    graph_x2.add(gtsam.BetweenFactorPose2(X(i), X(i + 1), ODOM, BETWEEN_NOISE))
initial_x2 = build_initial(drop_first=True)
result_x2 = optimize_graph(graph_x2, initial_x2, use_qr=True)
marginals_x2 = gtsam.Marginals(graph_x2, result_x2)

max_diff = 0.0
for i in range(2, NUM_POSES + 1):
    cov_eq = marginals_eq.marginalCovariance(X(i))
    cov_x2 = marginals_x2.marginalCovariance(X(i))
    max_diff = max(max_diff, np.max(np.abs(cov_eq - cov_x2)))

print(f"\nMax abs covariance entry diff (X2..X7): {max_diff:.3e}")

fig, ax = plt.subplots(1, 1, figsize=(6, 5))
plot_marginals(
    ax,
    result_x2,
    marginals_x2,
    pose_indices=range(2, NUM_POSES + 1),
    title="Prior on X2 after dropping X1",
)
ax.set_xlim(-3, 14)
ax.set_ylim(-3, 7)
plt.tight_layout()
plt.show()


Max abs covariance entry diff (X2..X7): 3.508e-14


# Show covariances for the last pose in Sections 4 and 5.
last_key = X(NUM_POSES)
cov_eq_last = marginals_eq.marginalCovariance(last_key)
cov_x2_last = marginals_x2.marginalCovariance(last_key)
print("\nSection 4 (NonlinearEquality) last pose covariance:\n", cov_eq_last)
print("\nSection 5 (Prior on X2) last pose covariance:\n", cov_x2_last)


Section 4 (NonlinearEquality) last pose covariance:
 [[0.3823628  0.52541169 0.06877334]
 [0.52541169 2.26703813 0.28962002]
 [0.06877334 0.28962002 0.06      ]]

Section 5 (Prior on X2) last pose covariance:
 [[0.3823628  0.52541169 0.06877334]
 [0.52541169 2.26703813 0.28962002]
 [0.06877334 0.28962002 0.06      ]]

Summary¶

Stronger priors tighten the marginal covariances throughout the chain.
A NonlinearEqualityPose2 produces a hard anchor on X(1).
Eliminating X(1) and converting the first between factor into a prior on X(2) yields matching marginals for X(2..7).